Algoritmo de Dijkstra
O algoritmo de Dijkstra, inicialmente, o usuário deve entrar com a matriz de custo do grafo. No entanto, este algoritmo considera que o grafo tem um vértice inicial. Assim, ele só calcula o caminho mínimo do vértice inicial para todos os outros. Portanto, o usuário deve definir em seguida qual é o vértice inicial. (final)
O algoritmo gera então dois vetores simples: 1)uma matriz de rota e 2)uma matriz de custo mínimo.
Leia (Custo[ ]); //ler matriz de custo
Leia (vert); //ler vértice inicial
Para i = 1 .. n faça // n é o número de vértices
Begin
Rota[i] = vert; // Rota do vértice inicial até o vértice i
Dist[i] = Custo[vert,i] // Custo inicial do vértice inicial até o vértice i
End
Para a = 1.. n faça
Para todo k Î G+(a) //Para todo vértice k que é sucessor do vértice a
Begin
P = mín(D[k], D[a]+Custo[a,k]);
If (P < D[k]) Then
Begin
Rota[k] = a;
Dist[k] = P;
End
Só lembrando que os vértices sucessores de a serão aqueles que têm um valor de custo diferente de 0 (ou seja, não é o próprio vértice) e diferente de ¥ (ou seja, não existe aresta entre eles e, portanto, o vértice não é um sucessor).
Considere por exemplo o seguinte grafo:
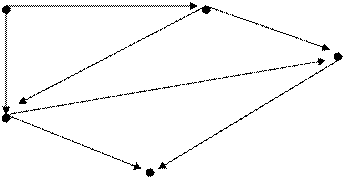 1 2
2
1 2
2
3
10
7 3
8
5 4
5
4
Inicialmente, o algoritmo solicita que o usuário entre a matriz de custo do grafo.
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
2 |
¥ |
¥ |
10 |
|
2 |
¥ |
0 |
3 |
¥ |
7 |
|
3 |
¥ |
¥ |
0 |
4 |
¥ |
|
4 |
¥ |
¥ |
¥ |
0 |
¥ |
|
5 |
¥ |
¥ |
8 |
5 |
0 |
Em seguida, pergunta qual é o vértice inicial. Vamos considerar que o vértice inicial é o vértice 1. Temos então:
Vert = 1
Rota[1,1,1,1,1].
Dist[0,2, ¥,¥,10]
Ou seja, inicialmente ele inicializa todas as posições do vetor Rota com o vértice inicial. Em seguida, coloca o custo das arestas do vértice inicial para todas as outras. Quando a aresta não existe, o valor ¥ é colocado.
a = 1, k=1 vértice 1 não é sucessor de 1
k=2 D[2] x D[1] + Custo[1,2] à 2 x 0+2 à p=2. p < D[k]?? 2 <2 ? Não!
k=3 vértice 3 não é sucessor de 1
k=4 4 não é sucessor de 1
k=5 D[5] x D[1] + Custo[1,5] à 10 x 0+10 à p=10 p < D[k]? 10 < 10? Não!
a = 2, k=1 vértice 1 não é sucessor de 2
k=2 vértice 2 não é sucessor de 2
k=3 D[3] x D[2] + Custo[2,3] à ¥ x 2+3 à p=5 p<D[k]? 5<¥? Sim!!
Rota[3]=2, Dist[3]=5
Rota[1,1,2,1,1] e Dist[0,2,5, ¥,10]
k=4 4 não é sucessor de 2
k=5 D[5] x D[2] + Custo[2,5] à 10 x 2+7 à p=9 p < D[k]? 9 < 10? Sim!
Rota[5]=2, Dist[5]=9
Rota[1,1,2,1,2] e Dist[0,2,5, ¥,9]
a = 3, k=1 vértice 1 não é sucessor de 3
k=2 vértice 2 não é sucessor de 3
k=3 vértice 3 não é sucessor de 3
k=4 D[4] x D[3] + Custo[3,4] à ¥ x 5+4 à p=9 p < D[4]? 9 < ¥? Sim!
Rota[4]=3, Dist[4]=9
Rota[1,1,2,3,2] e Dist[0,2,5, 9,9]
k=5 vértice 5 não é sucessor de 3
a = 4, k=1 vértice 1 não é sucessor de 4
k=2 vértice 2 não é sucessor de 4
k=3 vértice 3 não é sucessor de 4
k=4 vértice 4 não é sucessor de 4
k=5 vértice 5 não é sucessor de 4
a = 5, k=1 vértice 1 não é sucessor de 5
k=2 vértice 2 não é sucessor de 5
k=3 D[3] x D[5] + Custo[5,3] à 5 x 9+8 à p=5 p < D[3]? 5 < 5? Não!
k=4 D[4] x D[5] + Custo[5,4] à 9 x 9+5 à p=9 p < D[4]? 9 < 9? Não!
k=5 vértice 5 não é sucessor de 5
Assim, no final temos:
Rota[1,1,2,3,2] e Dist[0,2,5,9,9].
Exercício 1 – Para o mesmo grafo, repita o procedimento acima, mas considerando que o vértice inicial é o vértice 2.
Exercício 2 – Para o seguinte grafo, aplique o algoritmo “passo a passo”, de forma a descobrir a matriz de rota e a matriz de custo mínimo. Considere que o vértice 1 é vértice inicial. Determine então a pista do vértice 1 para todos os outros vértices
2 1 3

10
1 3 2 9 4 6
5 7
5 2 4