GEO LOGOS – 2021

1 Teoria dos Grafos

1.1 Introdução

Os grafos, ou problema em grafos, são estudados há muitos anos. Já em 1736, Euler descreveu o seguinte problema: Dada a configuração abaixo[1], tendo um rio com duas ilhas, duas margens e 7 pontes, é possível passar por todas as pontes sem repetir nenhuma? Como provar?

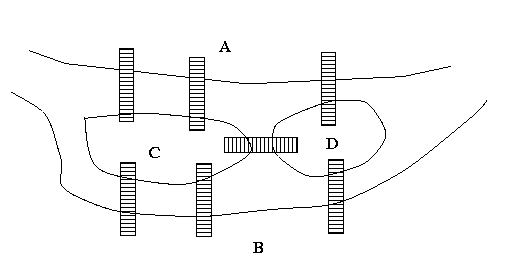
Para resolver esse problema, Euler o representou com o grafo ilustrado na Figura 1. Com essa representação, e considerando as propriedades dos grafos que serão apresentadas mais tarde nesse curso, é possível resolver facilmente esse problema.

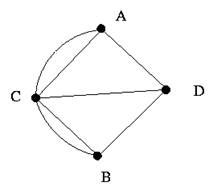
Figura 1 . Representação gráfica do problema de Euler

Esse tem sido considerado o primeiro problema do que hoje chamamos de teoria dos grafos. No entanto, até o fim do século 19 houve poucos trabalhos na área. Por exemplo, em 1847, Kirchhoff utilizou modelos de grafos no estudo de circuitos elétricos. Em 1857, Cayley utilizou grafos na química orgânica. Em 1859, Hamilton inventou um jogo que consistia na busca de um percurso fechado envolvendo todos os vértices de um dodecaedro regular, de tal modo que cada um deles fosse visitado uma única vez. Para mais exemplos, consulte, por exemplo, Boaventura Neto, 1996.

1.1.1 Representação Gráfica

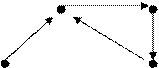
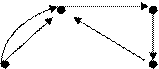
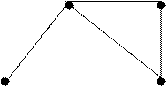
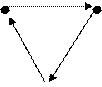
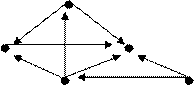
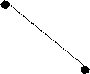
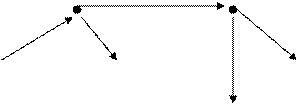
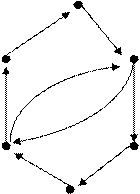
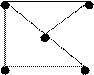
Visualmente, os grafos são representados por um conjunto de pontos e um conjunto de linhas ou setas ligando esses pontos. Exemplos:

Vértices – são os “pontos”, ou nós Arestas – são as linhas ou setas, ou arcos.

1.1.2 Representação Matemática

Um grafo G é definido como G(V,A) onde V é um conjunto finito e não vazio de vértices e A um conjunto finito de pares de V, isto é, A Ì (VxV). Os elementos de A são chamados de arestas do grafo.

1.1.3 Definições Básicas

· Laço – uma aresta que incide com um único vértice é chamada de laço.

· Orientação – é a direção para a qual uma seta aponta. Se a aresta não tiver seta, diz-se que ela não tem orientação

· Incidente – Diz-se que uma aresta é incidente com os vértices que ela liga (não importa a orientação).

· Vértices Adjacentes – dois vértices são adjacentes se estão ligados por uma aresta.

· Vértice isolado – Um vértice é dito isolado se não existe aresta incidente sobre ele.

· Arestas paralelas – Duas arestas incidentes nos mesmos vértices (não importa a orientação). Ou seja, se a1 = (v,w) e a2 = (v,w), então as arestas a1 e a2 são paralelas.

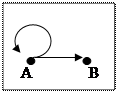
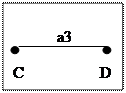
Laço no vértice A                                      A aresta a3 incide no vértice C e no vértice D.

Os vértices A e B são adjacentes. os vértices C e D também são adjacentes.

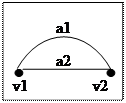
         Vértice E isolado.                                           As aresta a1 é  paralela

1.1.4 Tipos de Grafos

1.1.4.1 Grafo Rotulado

Um grafo é dito rotulado quando seus vértices e/ou arestas são distinguidos uns dos outros por rótulos (que pode ser um nome, um número ou conjunto de letras ou números. Caso contrário o grafo é não rotulado.

Nos exemplos abaixo, o primeiro grafo não tem nenhum rótulo. O segundo grafo possui rótulos nos vértices e o terceiro grafo possui rótulos nas arestas.

                                                         x1

                                                                                                        a1               a2

                                            x2                       x3

Grafo não rotulado                            Grafo rotulado                     Grafo rotulado

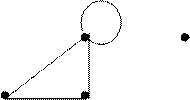
Exemplo 1 – Represente graficamente um grafo definido matematicamente como segue: Grafo G(V,A), onde V = {v1,v2,v3,v4} e A = {(v1,v2),(v2,v3),(v3,v3),(v3,v1)}.

Há varias formas gráficas semelhantes de se representar esse grafo, mantendo as definições, pois a posição dos vértices no espaço é irrelevante. Vou fazer de duas formas diferentes.

v4

v3

            v1                  v4                                                                             

v2

v1

        v2                    v3                                                                        

1.1.4.2 Subgrafos

Seja G(V,A) um grafo. Um subgrafo G’ de G é um grafo G’(V’,A’), tal que V’É V e A’É A.

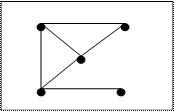
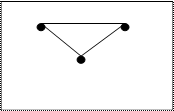
                                    Grafo G                                                          Grafo G’

1.1.4.3 Ordem

A ordem de um grafo é definida por |V| = n. Ou seja, a ordem de um grafo é o número de vértices.

1.1.4.4 Grafos simples, completos e multígrafos

· Multígrafo – grafo que contém arestas paralelas ou aços

· Grafo simples – grafo que não contém nenhum par de arestas paralelas ou laços.

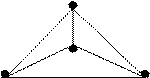
· Grafo completo – um grafo simples será completo quando existir uma aresta entre cada par de seus vértices.

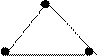
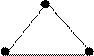
· Exemplos de grafos completos de 2, 3 e 4 vértices:

_n

§ Um grafo completo com n vértices possui m =    2    arestas ou (n-1)!

§ Um grafo completo de n vértices é denominado cliques.

1.1.4.5 Grafo Complementar

Um grafo G  é dito complementar de G se possui a mesma ordem de G e se uma aresta (v,w) Î G, então (v,w) Ï G e vice-versa. Exemplo:

                 Grafo G                                                    Grafo G

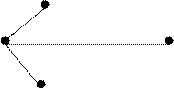
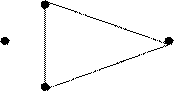                  a                                                                                 a

 b                                               d                                     b                                             d  

                  c                                                                                c

No caso de grafos dirigidos, o grafo complementar G será aquele que possui os mesmos vértices de G, possui todas as arestas não presentes em G e possui o reverso das arestas de G. Por exemplo:

                 Grafo G                                                                            Grafo G

                  a                                                                                 a

b                                               d                                     b                                             d  

c                                                                               

                                                                                                    c

1.1.4.6 Grafo Bipartite

Se G(V1 È V2,A) é tal que, para V1 Ç V2 = Æ e para toda aresta (vi,vj) Î A, tem-se que vi Î V1 e vj Î V2, então o grafo é denominado bipartite.

Ou seja, o grafo pode ser dividido logicamente em dois conjuntos de vértices, tal que toda aresta começa no vértice de um dos conjuntos e termina no vértice do outro conjunto.

                                                                       V1 = {a.,b}

                a                           c                         V2 = {c,d,e}

                                             d

                b                            e

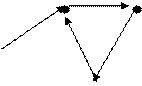
1.1.4.7 Grafo Dirigido

Um grafo é chamado de dirigido (ou dígrafo) se suas arestas possuem orientação. Caso contrário o grafo é não dirigido. Em termos leigos: será dirigido se suas arestas forem “flechas” que apontam o vértice inicial e final de cada aresta.

1.1.4.8 Grafos Isomorfos

Dois grafos são isomorfos se coincidirem os vértices de suas representações gráficas, preservando as adjacências das arestas. Em outras palavras, são isomorfos se têm a mesma representação matemática, mas são representados diferentemente graficamente.

Formalmente pode-se dizer que G1(V1,A1) e G2(V2,A2) são isomorfos se satisfizerem as seguintes condições:

1) |V1| = |V2| = n.

2) Existe uma função bijetora f: V1 àV2, tal que (v,w) Î A1 ó ((f(v),f(w)) Î A2 " v,w Î V1.

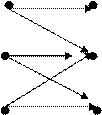
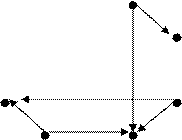a                            a’                                                                a

                                                                                                              a’

    b                              b’

     c                             c’                               c’                                                  b

                                                                                 c                          b’

1.1.4.9 Grau e Grafos Regulares

· O grau de um vértice v Î V denotado por gr(v) = número de arestas incidentes a v (sendo que um laço equivale a duas arestas).

· Um grafo é dito regular de grau r se todos os vértices possuem grau r. Ou seja, todos os vértices possuem o mesmo grau.

· Teorema 1 – A soma dos graus dos vértices de um grafo é igual a duas vezes o número de arestas.

· Teorema 2 – Em qualquer grafo existe sempre um número par de vértices de grau ímpar.

1.1.4.10 Grafo Valorado

Seja pi um número associado a cada aresta e qj um número associado a cada vértice de um grafo G(V,A). Então G é denominado de grafo valorado e o número pi é chamado de custo da aresta e o número qj é chamado de custo do vértice.

Custo da aresta pode significar distância, altitude, capacidade, fluxo etc.

Custo do vértice pode significar capacidade, entradas, etc.

                         10km

                                                 8km          16km

1.2 Sucessores e Antecessores de um Grafo Dirigido

Formalmente, os vértices sucessores e antecessores de um grafo dirigido são definidos da seguinte forma:

· v é sucessor de w <=> (w,v) Î A

· v é antecessor de w <=> (v,w) Î A

Os conjuntos de todos os vértices sucessores e antecessores de um dos vértices de um grafo são formalmente definidos da seguinte forma:

· G+(v) = {w/(v,w) Î A                 --> conjunto de sucessores de v

· G-(v) = {w/(w,v) Î A                  --> conjunto de antecessores de v

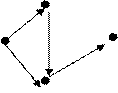
Exemplo:

                                               b

                                    a                                d

                                                    c

G+(a) = {b,c}              G+(b) = {c}                G+(c) = {d}                G+(d) = { }

G-(a) = { }                  G-(b) = {a}                 G-(c) = {a,b}              G-(d) = {c}

1.3 Representação de Grafos em um Computador

Para que um grafo seja armazenado em um computador, é necessário definir dois aspectos:

• Quais informações devem ser consideradas
• Como armazenar as informações no computador, ou seja, definir a estrutura de dados que será utilizada.

A estrutura de dados é particularmente importante, pois a eficiência de um algoritmo que irá trabalhar sobre o grafo vai depender da escolha certa de como representar o grafo.

De uma forma geral, pode-se representar um grafo utilizando matrizes ou listas, como veremos a seguir.

1.3.1 Matriz de Adjacência

Dado um grafo G(V,A), a matriz de adjacência A = [a_ij] é uma matriz n x n tal que

a_ij =    1 se e somente se existe (v_i, v_j) Î A_j

          0 caso contrário

Exemplo:

                   a2                    a4

     a1                                  a3

                  a2                      a3

a1                                           a4

                  b                      c

 a                                           d

	1	2	3	4
1	0	1	0	0
2	1	0	1	1
3	0	1	0	1
4	0	1	1	0

			j
		1	2	3	4
	1	1	1	0	0
i	2	0	0	1	0
	3	0	0	0	1
	4	0	1	0	0

			j
		1	2	3	4
	1	0	2	0	0
i	2	0	0	1	0
	3	0	0	0	1
	4	0	1	0	0

1.3.2 Matriz de Custo

Um grafo valorado pode ser representado por uma matriz de custo w = {w_ij}, onde

w_ij =    custo da aresta, se (v_i, v_j) Î A

¥ caso (v_i, v_j) Ï A (ou seja, caso não exista aresta)

Exemplo:

                     a2         2            a3

             1                                 8  

                                 5

  a1                                           a4

			j
		1	2	3	4
	1	¥	1	¥	¥
i	2	1	¥	2	5
	3	¥	2	¥	8
	4	¥	5	8	¥

1.3.3 Matriz de Incidência

Dado um grafo G(V,A) de n vértices e m arestas a matriz de incidência de G é denotada por B = [b_ij] é uma matriz n x m definida por:

b_ij =      1 se v_i é vértice de a_j

            0 caso contrário

Se o grafo G for orientado (dígrafo), então poderá ser definida como:

             1 se v_i for vértice inicial de a_j (ou se existir um laço no vértice vi)

b_ij =      -1 se v_i for vértice final de a_j

             0 se o vértice vi não pertence à aresta aj

Exemplo:

                   2           b             3

            a                                 c 

                             d

 1                                            4

            e

        1        a           2         b              3

                                  d               c

                                              4

			arestas
		a	b	c	d	e
	1	1	0	0	0	1
	2	1	1	0	1	0
vértices	3	0	1	1	0	0
	4	0	0	1	1	0

			arestas
		a	b	c	d
	1	1	0	0	0
	2	-1	1	0	-1
vértices	3	0	-1	1	0
	4	0	0	-1	1

1.3.4 Lista de Arestas

Pode-se representar um grafo em um computador utilizando-se duas listas de vértices, representando as arestas do grafo. As listas podem ser vetores simples.

A primeira lista contém os vértices de início de cada aresta.

A segunda lista contém os vértices onde cada uma delas termina. Por exemplo:

   v2                    v3

              v5                              L1 = (v2,v3,v3,v4,v5,v5)

                                               L2 = (v1,v2,v5,v3,v2,v4)

v1                        v4

1.3.5 Estrutura de Adjacência

Um grafo pode ser representado por uma lista de vértices e, para cada vértice da lista, é associada uma lista dos seus respectivos sucessores. Exemplo:

                  2

2

1

3

    1                                   3

3

-

5 4

			3

1.4 Caminho e Conexidade

1.4.1 Caminho

Formalmente temos o seguinte:

Definição: seja G(V,A) um grafo. Então define-se um caminho de G como sendo uma seqüência de arestas da forma (u,v),(v,w),(w,x),...,(y,z), onde cada aresta pertence ao grafo G.

O caminho denotado acima é definido, também, como o caminho entre u e z e pode ser representado por: u v w x ... y z.

O exemplo abaixo mostra um caminho entre d e c. O caminho é denotado por d a b c.

                                             a

               b                                                  c

                                      d                              e

1.4.2 Cadeia

Definição: uma cadeia é uma seqüência de arestas de um grafo G, tal que qualquer par de arestas subseqüentes possuem um vértice de incidência comum. Ao contrário da definição de caminho, uma cadeia ignora a orientação das arestas.

Portanto, todo caminho é uma cadeia, porém a recíproca nem sempre é verdadeira. Veja o seguinte exemplo:

           b

                                         A seqüência a b c d é um caminho, também uma cadeia.

      a                                     c       A seqüência a b d c é uma cadeia, mas não é um caminho.

                      d

Caminho: segue a orientação

Cadeia: não precisa seguir a orientação

1.4.3 Comprimento

Definição: o número de arestas k que compõem um caminho (ou cadeia) é denominado de comprimento do caminho (ou da cadeia). Exemplo.

                b

O caminho a b c d é um caminho entre ‘a’ e ‘d’ de comprimento igual a 3

a                                  c

                     d

1.4.4 Caminho Simples x Trajetória

Definição: se os vértices de um caminho (ou cadeia) forem distintos (com exceção do vértice inicial e o vértice final), então a seqüência recebe o nome de caminho simples (ou cadeia simples). Se as arestas da seqüência forem distintas, então a seqüência recebe o nome de trajeto ou trajetória. Exemplo:

                    2                     3

   1                     4                                A seqüência 1 2 3 4 5 é um caminho simples.

                                                           A seqüência 1 2 3 4 2 é uma trajetória.

                                                           A seqüência 1 2 3 4 2 1 é apenas uma seqüência.

  6                            5

1.4.5 Grafo Conexo

Definição: um grafo G é conexo se existe pelo menos um caminho (ou cadeia) entre qualquer par de vértices de G. Caso contrário o grafo é desconexo. Exemplo:

            a) Grafo conexo                                             b) Grafo desconexo

Todo grafo desconexo é composto por subgrafos conexos chamados de componentes. Por exemplo, o grafo b) é um grafo desconexo composto por 2 componentes.

1.4.6 Caminhos abertos e fechados

Um caminho em G é denominado fechado se o vértice final é o mesmo que o vértice inicial. Caso contrário, o caminho é denominado aberto. Exemplo:

                    b                        c

                                                           Caminho aberto: b d c e

    a                                                     Caminho fechado: b d c e b

                  e                    d

De forma semelhante a um caminho fechado, uma cadeia fechada de um grafo é uma cadeia de G tal que a aresta inicial e a aresta final possuem um vértice de incidência em comum, ou em outras palavras, se o vértice inicial e o vértice final se confundem.

1.4.7 Circuito e Ciclo

Um circuito é um caminho simples fechado.

Um ciclo é uma cadeia simples fechada. Exemplo:

                        b                  c

                                                                       Circuito: a b c d a

    a                                                                 Ciclo: d c b d

                                    d

Um grafo que não contém nenhum ciclo é chamado de “grafo acíclico”.

1.4.8 Algoritmo de Goodman

Esse algoritmo verifica se um grafo é conexo e identifica seus componentes no caso de ser desconexo. A idéia consiste em reduzir cada componente a um único ponto. Nesse algoritmo necessitamos da definição de fusão de dois vértices

Fusão – Dados dois vértices u e v adjacentes de um grafo G, a fusão de v com u é feita eliminando-se a aresta (v,u) e em seguida tornando v e u um único vértice. O vértice resultante desta fusão é um vértice w adjacente a todos os vértices anteriormente adjacentes a u e/ou v. Exemplo:

               a                        b                                                      a                        b

                                               Após a fusão de u e v à

    u                        v                                                                        w           

O procedimento consiste da escolha de um vértice inicial v0 e a fusão de um vértice com ele. Isto é repetido até que não reste qualquer vértice adjacente a v0. Caso reste algum vértice não adjacente a v0, então novo vértice v0 é selecionado e o processo é repetido. Se no final o grafo resultante for apenas um vértice, então o grafo é conexo. Caso contrário, o número de vértices representará o número de componentes do grafo.

Entrada: grafo G(V,A)

Saída: variável c contendo o número de componentes.

P0. [inicialize] H ß G; c ß 0;

P1. [Gere a próxima componente]

      Enquanto H ¹ 0 faça

             Selecione um vértice v0 Î H;

             Enquanto v0 for adjacente a algum vértice u Î H faça

                     H ß grafo resultante da fusão de u com v0.

             Remova v0, isto é, faça H ß H – v0;

                                                   c ß c + 1;

P2.[Teste do Tipo de conexidade]

      Se c>1 então G é desconexo.

      Senão G é conexo.

Exemplo:

                  a                      b

f                      e                             1^o. passo: escolher um vértice.

            Vértice d. Fusão de d com e.

     c                       d

               a                          b

  f                                                        Vértice d. Fusão de d com c.

   c                         d

  a                          b               

 f                                                         Vértice d. Fusão de d com b.

                              d

   a                  

  f                                                        Vértice d. Fusão com a.

                            d

              d

f

1.5 Localização de Centros (em grafos não valorados)

1.5.1 Distância

Dados dois vértices v e w pertencentes ao grafo G(V,A), denomina-se distância entre v e w, o comprimento do menor caminho entre dois vértices v e w. No caso da não existência desse caminho, considera-se a distância infinita.

Notação: d(v,w) = distância entre os vértices v e w

                            = comprimento do menor caminho entre v e w

Denotamos por D(G) a matriz de distâncias de um grafo, onde dij=(vi,vj)

Em um grafo conexo, distância é uma métrica, isto é, para todo vértice de G(V,A) tem-se que:

i) d(u,v)>=0 com d(u,v)=0 se e somente se u=v.

ii) d(u,v) = d(v,u)  ocorre apenas quando o grafo é não orientado;

iii) d(u,v) + d(v,w) >= d(u,w)

1.5.2 Pista

Uma pista P(xi,xj) ou P(ij) ou Pij é um caminho de comprimento mínimo entre xi e xj, ou seja, um caminho de comprimento igual a d(xi,xj). Por exemplo, considere o grafo abaixo:

                        b                                      f

   a                                  c                                            g

                        d                                     e

            Qual a distância entre a e g?

d(a,g) = 3,       P(a,g) = (a,b,f,g)        P(a,e) = (a,b,f,e) ou (a,c,d,e)

1.5.3 Excentricidade

A excentricidade de um vértice v, denotado por e(v), é a máxima das distâncias d(v,u), isto é:

e(v) = Max{d(v,u), "u Î G}

Em outras palavras, a excentricidade de um vértice v é a maior distância existente a partir de v.

1.5.4 Raio

O raio de um grafo G, denotado por r(g), é o mínimo das excentricidades dos vértices de G Min(e(v)). Assim, r(G) = Min{e(v), "v Î G}.

1.5.5 Centro

O centro de um grafo G é definido pelo conjunto de vértices v tais que e(v) = r(g), isto é, centro = {v Î G / e(v) = r(G) }.

Em uma rede de comunicação, a localização de um ponto importante (uma rede de transmissão, por exemplo) em um centro do grafo que representa a rede é, a priori, uma providência no sentido de procurar reduzir ao máximo o número de transmissões de mensagens ou de equipamentos de conexão envolvidos.

Exemplo: localizar o centro do grafo abaixo.

   a                            b

                                               c          

   e                            d

	a	b	c	d	e	e(v)
a	0	1	1	2	1	2
b	1	0	1	2	2	2
c	1	1	0	1	1	1
d	2	2	1	0	1	2
e	1	2	1	1	0	2

raio = r(G) = 1

centro = {c}

1.5.6 Centro de um grafo dirigido

Em um grafo dirigido, define-se excentricidade de um vértice v por

es = Max{d(v,u), "u Î G}

Define-se excentricidade de retorno de um vértice v por

er = Max{d(u,v), "u Î G}

O raio de um dígrafo G é definido por:

r(G) = Min{es(v), er(v)}

Centro de um dígrafo G é definido pelo conjunto de vértices v tais que

es(v) = r(G) ou er(v) = r(G), isto é:

centro = {v Î G / es(v) = r(G) ou er(v) = r(G)}

Por exemplo, localize o centro do grafo G abaixo:

 a                        b

                                           c

e                          d

	a	b	c	d	e	es(v)
a	0	1	1	2	2	2
b	3	0	1	2	2	3
c	2	3	0	1	1	3
d	2	3	3	0	1	3
e	1	2	2	3	0	3
er(v)	3	3	3	3	2

raio = r(G) = 2

centro = {a,e}

1.5.7 Localização de Centros de Emergência

Aqui o interesse é determinar o centro de um grafo de tal modo que o tempo de ida e de volta seja mínimo (é o caso da localização de hospitais, polícia, bombeiro, etc). Observe que, neste caso, os vértices representam uma população e, como tal, devem ser levados em consideração.

Definição: A excentricidade de saída e retorno de um vértice é definida por:

esr(xi) = Max {pj [d(xi,xj) + d(xj,xi)]}

            onde j é o peso do vértice xj. Este peso pode ser entendido como a importância do vértice. Por exemplo, para localização de um hospital, o tamanho da população num bairro pode ser uma informação importante.

Definição: O raio de um grafo G considerando ida e volta é definido por r(G) = Min{esr(xi)}.

Definição: O centro de emergência de um grafo G é definido pelo conjunto de vértices v tal que esr(v) = r(G). Centro de emergência = {v Î G/ esr(v) = r(G)}

Por exemplo, considere o seguinte dígrafo. Localize o centro de emergência do grafo.

                      x1         

   x6                                    x2

  x5                                     x3

x4

D(G)

x1	x2	x3	x4	x5	x6
0	1	2	3	2	3
3	0	1	2	1	2
4	3	0	1	2	3
3	2	3	0	1	2
2	1	2	3	0	1
1	2	3	4	3	0

D^T

x1	x2	x3	x4	x5	x6
0	3	4	3	2	1
1	0	3	2	1	2
2	1	0	3	2	3
3	2	1	0	3	4
2	1	2	1	0	3
3	2	3	2	1	0

D(G) + D^T

x1	x2	x3	x4	x5	x6	esr
0	4	6	6	4	4	6
4	0	4	4	2	4	4
6	4	0	4	4	6	6
6	4	4	0	4	6	6
4	2	4	4	0	4	4
4	4	6	6	4	0	6

Como o peso de cada vértice é igual a 1, então podemos calcular a excentricidade diretamente da matriz D(G) + D^T(G). Portanto, o centro de emergência do grafo é formado pelo conjunto {x2,x5}.

Exercícios:

1 – Desenhe o grafo cuja matriz de adjacência é dada por:

                                                    1       2       3      4    5     6

0	1	1	0	0	1
1	0	1	0	1	0
1	1	0	1	0	0
0	0	1	0	1	1
0	1	0	1	0	1
1	0	0	1	1	0

2 – Desenhe o grafo a partir da lista de adjacência:

3 – Localize o centro dos grafos abaixo. Para isso, determine o raio do grafo e a excentricidade dos vértices.

                                                                                                          a

             a                        b

                          c                                                                                              b

            d                         e                              c                                                d

                                                                                   e                           f

---